You should test your solver on three different IVP:s. First
Create a program for solving general IVP with backward Euler (a frame of
the program can be found in BackwardEulerNewton.m). You should
use Newton iterations for solving the implicit difference equation
that arises when computing ![]() from
from ![]() .
.
You should test your solver on three different IVP:s. First
Compare your result to the exact solution.
The second example is a stiff IVP,
``Akzo-Nobel system of chemical reactions''. Find the concentrations
![]() such that for
such that for ![]() ,
,
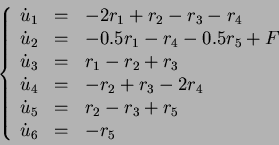 |
(4) |
The third and last example is the ``Volterra-Lotka'' equations, also
known as the prey-predator equations,
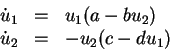 |
(5) |
Question 2 Can you notice any damping of the solution? What may be the cause of this?