


Next: Preparations
Up: Adaptive dG0 using duality
Previous: Adaptive dG0 using duality
The dG0 timestep method (backward Euler) for the initial value problem
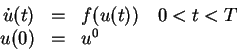 |
(1) |
is, Find 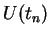 successively for
successively for 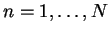 according to
according to
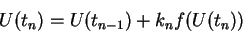 |
(2) |
The dual linearized problem is
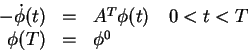 |
(3) |
where
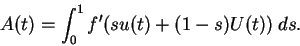 |
(4) |
Note that the dual problem
runs backward in time, starting at 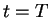 .
Replacing
.
Replacing  by
by  gives the approximate formula for
gives the approximate formula for

 |
(5) |
An adaptive scheme for solving the IVP could be formulated as,
choose an appropriate step length  such that
such that
 |
(6) |
where  is your error tolerance,
is your error tolerance,  the
stability factor defined by
the
stability factor defined by
 |
(7) |
where  solves (3).
solves (3).
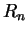 is the residual. A more useful approximation is to use
is the residual. A more useful approximation is to use  instead
of
instead
of 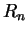 .
.



Next: Preparations
Up: Adaptive dG0 using duality
Previous: Adaptive dG0 using duality
Christoffer Cromvik
2004-04-26
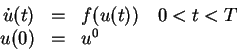
![]() successively for
successively for ![]() according to
according to
![]() such that
such that

